учитель математики и информатики
МОУ Аннинская СОШ №3 с УИОП
Воронежская область
Цели урока:
Образовательные:
- Обобщить и систематизировать знания учащихся по данной теме.
- Отработать навыки применения формул сокращённого умножения при решении заданий.
- Подготовиться к контрольной работе.
Развивающие:
- Развивать познавательный интерес и расширять кругозор учащихся.
- Научить применять знания на практике.
Воспитательные:
- Воспитывать в учащихся умения и навыки работы в коллективе.
Тип урока: урок обобщающего повторения.
Оборудование: мультимедийная установка.
Ход урока
Слайд №1-2
1. Организационный момент
Слайд №3
“Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами”.
И.Ньютон
Слайд №4
2. Знакомство с правилами игры «Математический морской бой».
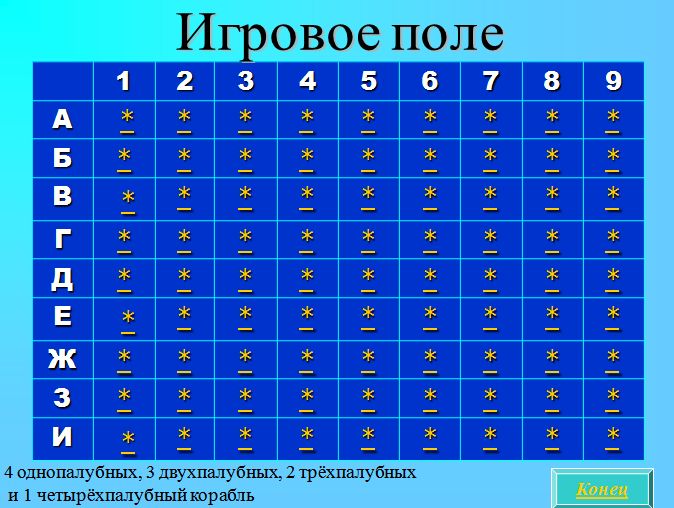
- Для проведения игры класс разбивается на 2 группы. Команды поочередно «стреляют» в корабли, называя ячейки игрового поля (слайд 5). Нажимая на символ * в указанной ячейке, проверяется результативность хода.
- Если одна из команд допустила промах, происходит переход хода (слайд 6), если выпадает историческая справка, после ознакомления с ней команда имеет право на очередной ход, при попадании всем командам предлагается задание. Первоочередное право ответа у той команды, которая сделала результативный ход. Если эта команда допускает ошибку, отвечают соперники. Баллы начисляются команде, давшей правильный ответ.
- Время выполнения задания ограниченно. По истечении отведенного времени проверяем ответ. Нажатием на слово «очки» мы переходим к таблице результатов (слайд 25) и вписываем баллы команде, правильно выполнившей задание. Затем, нажав на слово «обратно» вновь возвращаемся к игровому полю (слайд 5).
Слайд №5
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
А |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
Б |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
В |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
Г |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
Д |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
Е |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
Ж |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
З |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
И |
* |
* |
* |
* |
* |
* |
* |
* |
* |
3. Задания для выполнения
Вопросы для устной работы.
Слайд №7
А-1. Чему равна разность квадратов двух выражений? (2 балла)
Слайд №8
А-5. Чему равен квадрат суммы и квадрат разности двух выражений? (2 балла)
Слайд №9
А-6. Чему равна сумма кубов и разность кубов двух выражений? (2 балла)
Слайд №10
А-7. Чему равен квадрат суммы трёх выражений? (2 балла)
Слайд №11
А-9. Чему равен куб разности и куб суммы двух выражений? (2 балла)
Задания для выполнения в тетради.
Слайд №12
Б-1. Представьте в виде многочлена выражение(2m+5)(5-2m)+4m2 (4 балла).
Ответ: 25
Слайд №13
В-3. Представьте в виде многочлена выражение (2х+3)2 — 4х2 (4 балла).
Ответ: 12х+9
Слайд №14
В-4. Представьте в виде многочлена выражение(2х-3у)2 +(3х+2у)2 (4 балла).
Ответ: 13х2+13у2
Слайд №15
В-5. Представьте в виде многочлена выражение (2х-3)(2х+3)-(2х-1)2 (4 балла).
Ответ: 4х-10
Слайд №16
В-6. Представьте в виде многочлена выражение (2х+у)3-6ху(2х+у) (4 балла).
Ответ: 8х3 +у3
Слайд №17
В-9. Представьте в виде многочлена выражение (m-n)3 +3mn(m-n) (4 балла).
Ответ: m3 +n3
Слайд №18
Д-8. Разложите на множители многочлен (2х+1)2 -16 (6 баллов).
Ответ: (2х-3)(2х+5).
Слайд №19
Е-2. Разложите на множители многочлен (х -2)2-(х+1)2 (6 баллов).
Ответ: -3(2х-1)
Слайд №20
Ж-4. Представьте в виде произведения х6 -27 (8 баллов).
Ответ: (х2-3)(х4+3х2+9)
Слайд №21
Ж-5. Преобразуйте в многочлен(3х+у2)3 (8 баллов).
Ответ: 27х3+27х2у2+9ху4+у6
Слайд №22
З-7. Решите уравнение: 4х2+4х+1=0 (10 баллов).
Решение
4х2+4х+1=0
(2х+1)2=0;
2х+1=0;
2х=-1;
х=1:2;
х=0,5.
4·0,52 + 4·0,5+1=0.
0=0
Ответ: 0,5
Слайд №23
З-8. Решите уравнение: (7-х)2-(х-8)(х+8)=43 (10 баллов).
Решение.
(7-х)2-(х-8)(х+8)=43;
72-2·7·х+х2–(х2 -82)=43;
49-14х+х2-х2+44=43;
-14х=-70;
х=-70:14;
х=5.
(7-5)2-(5-8)(5+8)=43
43=43.
Ответ:5
Слайд №24
И-2. Найдите наименьшее значение квадратного трёхчлена х2 +2х+7 (12 баллов).
Решение.
х2 +2х+7=(х2 +2·1·х+12)-12+7=(х+1)2+6
Данный трёхчлен принимает наименьшее значение, когда (х+1)2 принимает наименьшее значение, т.е. (х+1)2=0.
Следовательно, наименьшее значение квадратного трёхчлена равно 6.
Ответ: 6
Слайд №25
И-3. При каком значении х любых значениях х квадратный трёхчлен х2-12х+50 принимает наименьшее значение? (12 баллов).
Решение.
х2-12х+50=(х2-2·6·х+36)-36+50 = (х-6)2+14
Данный трёхчлен принимает наименьшее значение, когда
(х-6)2=0;
х-6=0;
х=6.
Ответ: 6
Слайд №26
И-4. Приз. (6 баллов).
4. Исторические справки
Поскольку формулы сокращённого умножения мы изучаем на уроке алгебры, то данные исторические справки позволят вам узнать о том, откуда пошло это название и какие учёные внесли большой вклад в развитие этой науки.
Слайд №27
- Слово «Алгебра» возникло после появления трактата математика и астронома Мухаммеда бен Муса аль-Хорезми (787-ок.850). Термин «аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как алгебра.
Слайд №28
- Мухаммед Аль-Хорезми (787 –около 850) написал основополагающие трактаты по арифметике и алгебры.
Слайд №29
- Диофант Александровский (III век). В его книге «Арифметика» появляются зачатки буквенной символики и специальные обозначения для степеней, а также знак равенства, краткая запись правил умножения, задачи, приводящие к сложным системам алгебраических уравнений
Слайд №30
- Франсуа Виет (1540-1603) ввёл алгебраические символы, стал числа обозначать буквами, разработал основы алгебры
Слайд №31
- Пьер Ферма (1601-1665) занимался теорией решения алгебраических уравнений с несколькими переменными
Слайд №32
- Рене Декарт (1596-1650) расширил запас чисел, с которыми можно было производить действия. Ввёл :x, y, z — переменные, неизвестные; a, b, c — постоянные, параметры; знак деления.
Слайд №33
- Готфрид Вильгельм Лейбниц (1446-1716) создал основы математического анализа, ввел многие понятия и символы
Слайд №34
5. Итог урока. Подсчёт баллов и награждение команды – победителя.
Слайд №35
Проверка расположения кораблей.
6. Домашнее задание


{module Google_kvadrat}
Презентация в формате .ppt и конспект урока в формате .doc объемом 2,54 Mb





